数学秘籍3—万变不离其宗的图形变换
2019-11-19 10:29
来源:河北新高考
作者:新东方数学组
数形结合在解决中学数学问题中占有极其重要的地位,在历年的高考中也十分重视对数形结合的考查,考纲中强调“在高考中,充分利用选择题和填空题的题型特点,为考查数形结合的思想提供了方便,能突出 考查学生将复杂的数量关系转化为直观的几何图形问题来解决的意识”。以坐标系为纽带使数学的解析式与函数图象、方程与曲线建立一一对应关系,从而对数量关系的研究可转化为对图形性质的研究,反之亦然;由“形”向“数”的转化往往比较明显,而由“数”到“形”的转化却需要转化的意识,并且高一上学期主要以代数知识为主,所以本次专题主要以“数”向“形”的转化为 主,利用“形”的直观性,实现数形结合,常与以下内容有关:
1.实数与数轴上的点的对应关系;
2.函数与图象的对应关系;
3.曲线与方程的对应关系;
4.以几何元素和几何条件为背景,建立起来的概念,如复数、三角函数等.
高一上学期函数是重点,所以本次专题课主要针对函数与图象的对应关系,由于函数与方程是天然的“搭档”,所以还会涉及函数零点、方程解、及图象交点的三者转化,其中图象是解决函数类问题的关键,也是“形”的重要体现.题型一:函数的图像变换
图象变换是建立在基本初等函数与复杂或复合函数之间的桥梁,也是理解复杂或复合函数的重要手段,在高中阶段要求重点掌握,图象的基本变换有:平移变换、伸缩变换、翻折变换和对称变换.

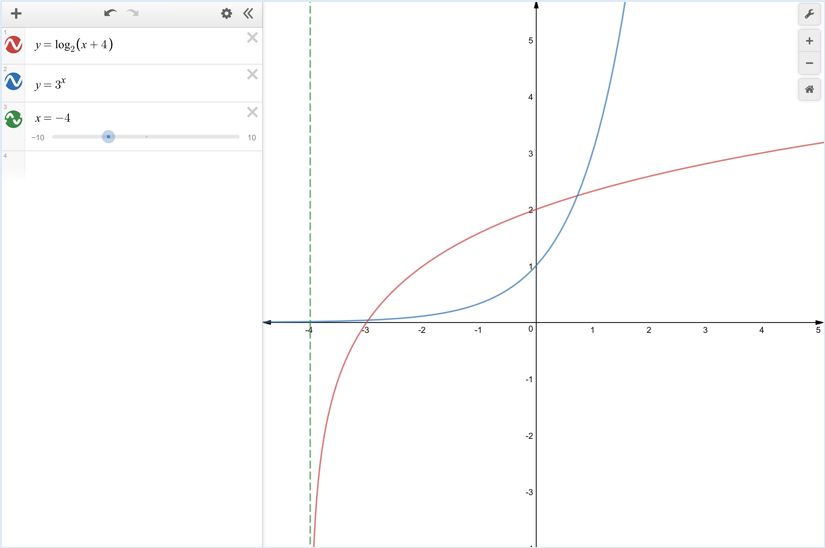
注:本题可以从代数角度解决,从代数角度来说:可借助分类讨论打开绝对值符号进行分类,求出各种情况下的解析式,进而求出解集,但是由于情况过多,需要求出四个区间内的解析式和解集,操作太过繁琐,是否还有其他办法呢?




练习一:

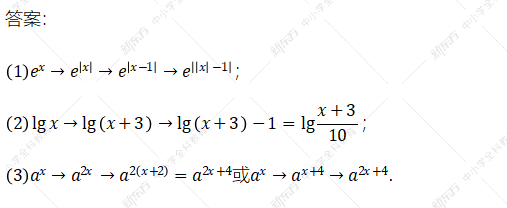
练习二:

备注:在进行图象变化的过程中,要时刻注意特殊点和特殊线的变化:1、特殊点:极值点、与坐标轴交点;2、特殊线:渐近线。

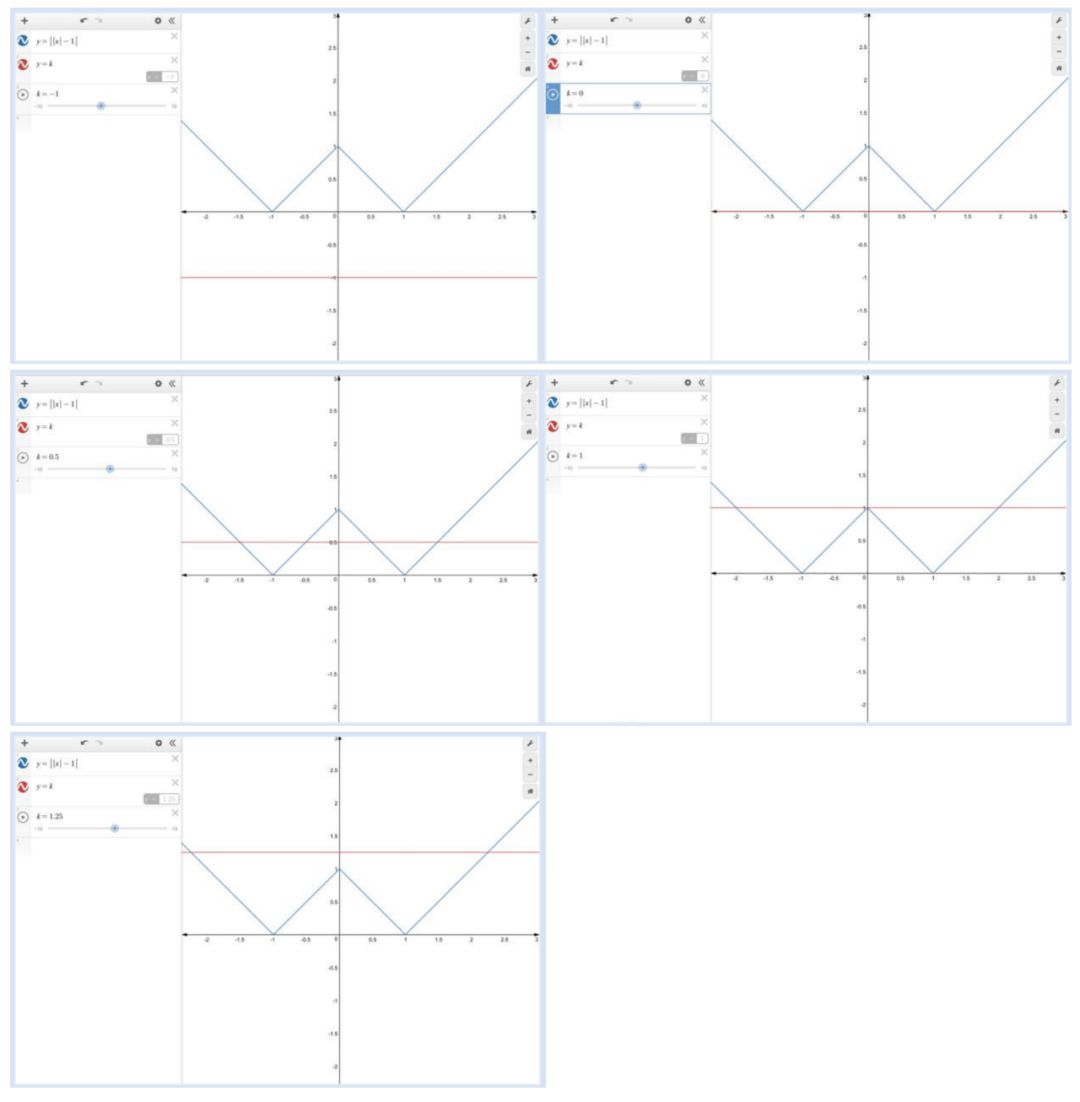
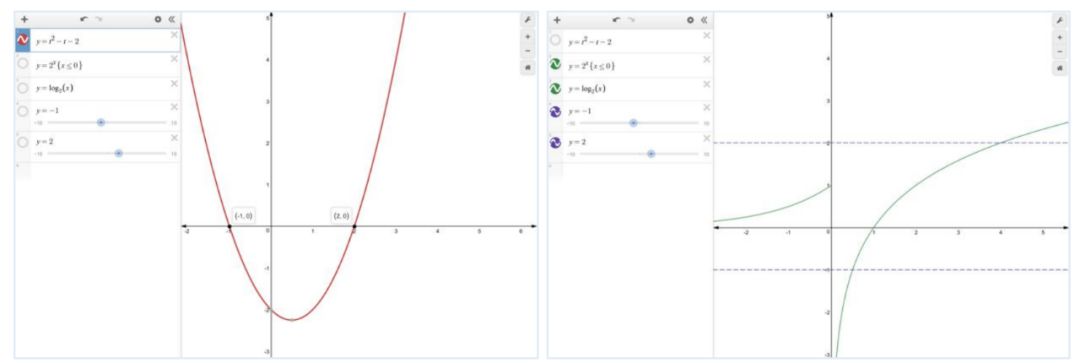
题型二:函数的零点问题











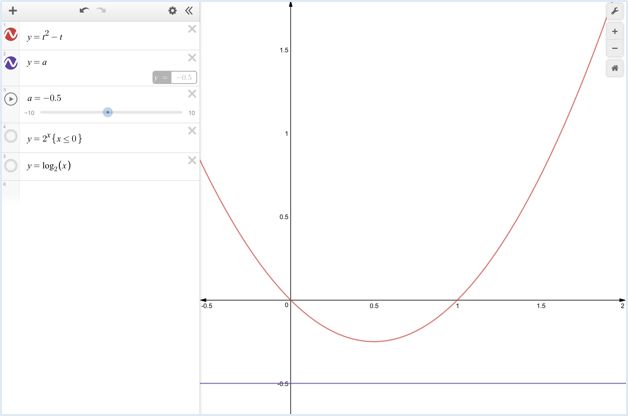

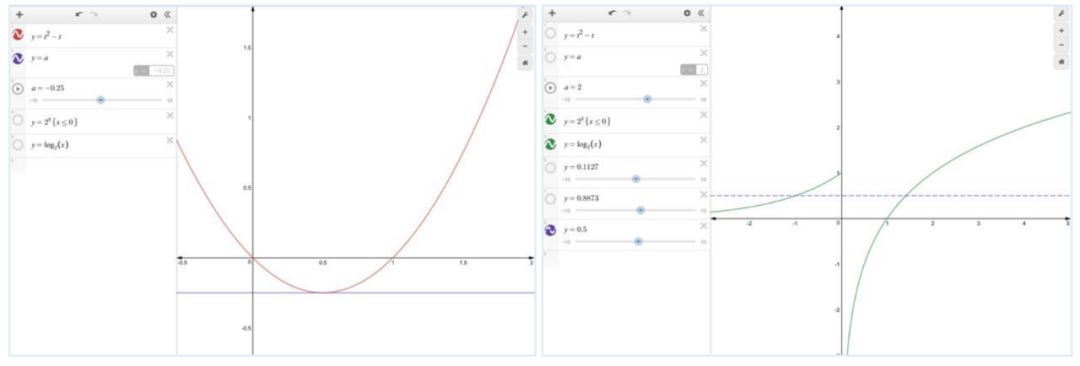

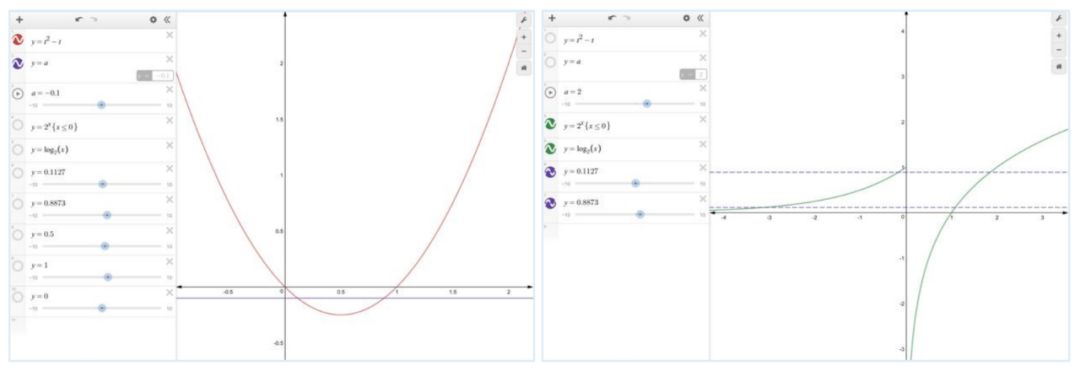

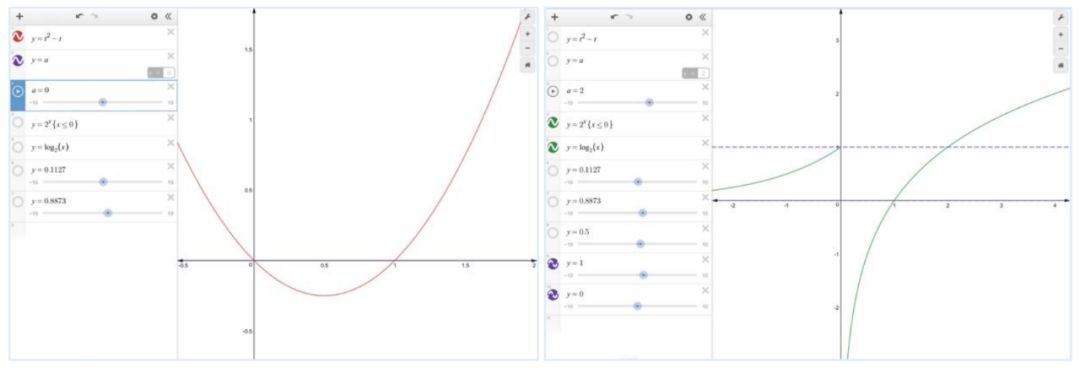


新东方石家庄学校 (微信号:helloxdf)
及时获取本地权威教育资讯,随时随地的贴身学习顾问,英语学习的好帮手、课程规划的好助手!
相关推荐
版权及免责声明
①凡本网注明"稿件来源:新东方"的所有文字、图片和音视频稿件,版权均属新东方教育科技集团(含本网和新东方网) 所有,任何媒体、网站或个人未经本网协议授权不得转载、链接、转贴或以其他任何方式复制、发表。已经本网协议授权的媒体、网站,在下载使用时必须注明"稿件来源:新东方",违者本网将依法追究法律责任。
② 本网未注明"稿件来源:新东方"的文/图等稿件均为转载稿,本网转载仅基于传递更多信息之目的,并不意味着赞同转载稿的观点或证实其内容的真实性。如其他媒体、网站或个人从本网下载使用,必须保留本网注明的"稿件来源",并自负版权等法律责任。如擅自篡改为"稿件来源:新东方",本网将依法追究法律责任。
③ 如本网转载稿涉及版权等问题,请作者见稿后在两周内速来电与新东方网联系,电话:010-60908555。