@高一,10分钟帮你搞定期中数学重难点!建议收藏!
2019-11-08 16:42
来源:河北新高考
作者:新东方数学组
高中数学必备的五大能力
通过高一第一个月的学习,所有的同学都已经见识到函数的威力,与初中函数相比较,高中函数抽象性和理论性突突突突然变强,解题思路和过程也更加复杂,这疾风骤雨般的变化让很多同学措手不及。但,河有两岸,事有两面,函数的强大,也令人升腾起一番敬意,有一说一,函数作为高中数学金字塔顶尖的存在,还是值得这份敬意的。下一阶段,期中考前,基本初等函数又会如约而至,别怕别慌,我就在新东方——“疾风知劲草,板荡识诚臣。”2018年高考数学考试大纲要求学生需要具备五大能力:空间想象能力、抽象概括能力、推理论证能力、运算求解能力、数据处理能力。高一的第一次月考考察四项能力:抽象概括能力、推理论证能力、运算求解能力,数形结合能力。下面以抽象概括能力和推理论证能力为例,给大家说一说到底是怎么一回事。抽象概括能力抽象概括能力:抽象是指提取题型本质的思维方法;概括是指把这种本质的思维方法,推及到其它同类事物上去,从而归结全类事物的共性的思维方法。
例1:已知奇偶性求函数解析式

此题是已知函数奇偶性求函数解析式的常规考法,平时练习过很多次,一般学生都不存在问题。如果孩子具备抽象概括的能力,能够提取此种类型题的本质思维,归结共性方法,那么下面的类奇偶函数求函数解析式的题目也能迎刃而解。例2:类奇偶性求函数解析式
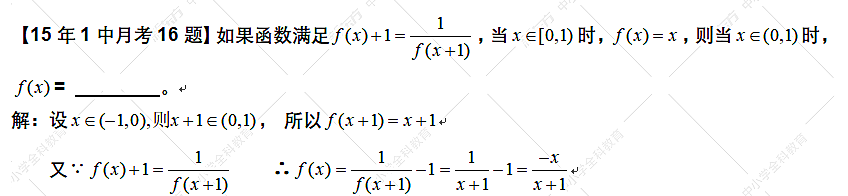
仅从题干上分析例1、例2,会发现这两道题是不同的,例题1依托的是函数的奇偶性,例题2完全抛开奇偶性,乍看不知道在考察什么知识。但是分析方法和步骤(黄色),会发现例1、例2具有相同的本质思维,和共性方法.从例题1到例题2的过程就是抽象概括的过程。抽象概括能力在短时间内难以成形,需要长时间训练。平时学习时需要深入挖掘,提取本质思维,更需要专业的老师针对性辅导。推理论证能力
推理论证能力:是一种由已知推断未知的思考活动,而反映这种思维活动的思维形式就是推理,反映形式为证明。
例:定义法证明函数单调性

平时训练时切忌跳步,因为在推理论证(证明)时学生需要运用数学语言的连续性、严密性和逻辑性,一旦跳步,数学语言将不再连续,极易出现错误,但这种错误,学生都会后知后觉,以为自己是会的,只是当时不细心。一旦形成错误归因,就会阻碍自己的进步。建议:所有问题尤其是证明问题不跳步。
高一期中考前必做的12道函数经典例题
1.最高次含参数,注意参数是否为0
 【题目分析】由题中“只有一个元素”可知,最高次数含有参数问题,首先让参数取零;其次参数不为零。方程有唯一解,故由判别式为零可得的值。【解答过程】
【题目分析】由题中“只有一个元素”可知,最高次数含有参数问题,首先让参数取零;其次参数不为零。方程有唯一解,故由判别式为零可得的值。【解答过程】

【题型反思】此题考查含参数的集合问题,关键要找到题目中参数与条件的关系,此题中参数作为集合里方程的系数,条件是方程的由唯一解,所以用方程根的判别式可求解。2.抽象函数求定义域问题

【题目分析】![]() 【解答过程】
【解答过程】

【题型反思】此题考查抽象函数(没有具体解析式的函数)求定义域,解决此类题型需注意以下两点:①函数的定义域为单个的取值范围;②只要函数的对应法则不变,则所对应的括号里面的范围不变。数学学习过程中需注意对基本概念的理解。3.函数求值域(一直在考,一直在错)

【题目分析】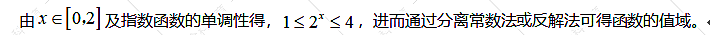 【解答过程】
【解答过程】

【题型反思】此题考查分式型函数求值域,此类题型一般有以下几种解法:①分离常数法(适用于齐次分式);②反解法(适用于有界函数组成的分式);③均值不等式法(适用于二次型分式);④判别式法(适用于二次型分式)。此外还可以采取定义证明(这是个很特别的方法)
 【答案】
【答案】

【解析】

4.求函数解析式

【题目分析】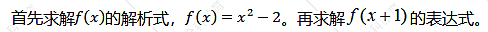 【解答过程】
【解答过程】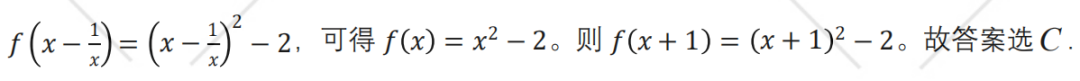
【题型反思】要熟练掌握抽象函数解析式的三种求法(换元法,代特殊值验证,构造)5.复合函数求值(注意自变量的取值范围)

【题目分析】 【解答过程】
【解答过程】 【题型反思】解决此类问题的关键是熟悉解析式特征与所求不等式的结构。6.抽象函数解不等式
【题型反思】解决此类问题的关键是熟悉解析式特征与所求不等式的结构。6.抽象函数解不等式

【题目分析】 【解答过程】
【解答过程】 【题型反思】本题给出满足特殊条件的抽象函数,求函数的值并解关于x的不等式,着重考查了抽象函数的理解和不等式的解法等知识点,属于中档题7.代特殊值求参数问题
【题型反思】本题给出满足特殊条件的抽象函数,求函数的值并解关于x的不等式,着重考查了抽象函数的理解和不等式的解法等知识点,属于中档题7.代特殊值求参数问题 【题目分析】
【题目分析】 【解答过程】
【解答过程】 【题型反思】含参数的奇偶性问题常用赋值法。8.单调奇偶综合(高中函数最最最最重要考法)
【题型反思】含参数的奇偶性问题常用赋值法。8.单调奇偶综合(高中函数最最最最重要考法)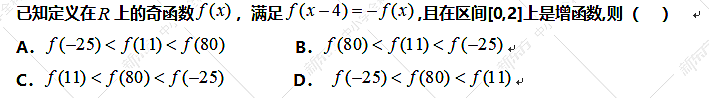 【题目分析】
【题目分析】 【解答过程】
【解答过程】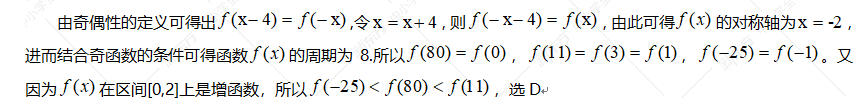 【题型反思】单调性与奇偶性综合问题,常见操作步骤:第一由函数的奇偶性优先补全函数的图像,第二注意单调性与周期性综合问题,常见的周期公式必须理解背诵啊。
【题型反思】单调性与奇偶性综合问题,常见操作步骤:第一由函数的奇偶性优先补全函数的图像,第二注意单调性与周期性综合问题,常见的周期公式必须理解背诵啊。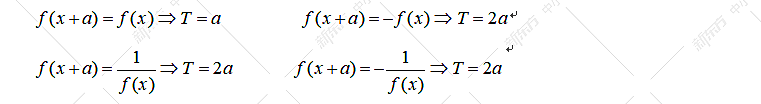 当然,如果出现与年份相关问题,多数考周期。9.分段函数的单调性
当然,如果出现与年份相关问题,多数考周期。9.分段函数的单调性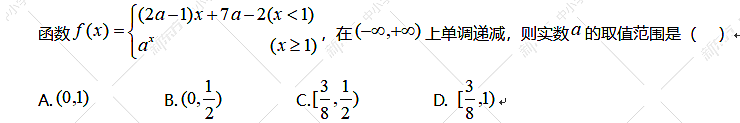 【题目分析】本题考查一次函数和指数函数以及分段函数的单调性,属于比较难的题目。【解答过程】
【题目分析】本题考查一次函数和指数函数以及分段函数的单调性,属于比较难的题目。【解答过程】 【题型反思】本题大部分同学会想到让一次函数和指数函数分别为减函数,进而选B,这样做没有考虑到分段函数的单调性,忽略了让一次函数的最小值大于等于指数函数的最大值,以后要引起注意。10.抽象函数单调性与奇偶性的证明
【题型反思】本题大部分同学会想到让一次函数和指数函数分别为减函数,进而选B,这样做没有考虑到分段函数的单调性,忽略了让一次函数的最小值大于等于指数函数的最大值,以后要引起注意。10.抽象函数单调性与奇偶性的证明 【解析】解析式赋值法类型条件结合定义法证明函数单调性是常见的第一次月考压轴题目
【解析】解析式赋值法类型条件结合定义法证明函数单调性是常见的第一次月考压轴题目 【题型反思1】
【题型反思1】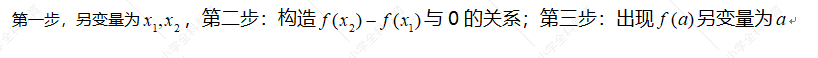 【题型反思2】
【题型反思2】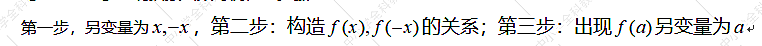 11.集合子集问题(注意子集的变形及正难则反的原则解决复杂问题)
11.集合子集问题(注意子集的变形及正难则反的原则解决复杂问题)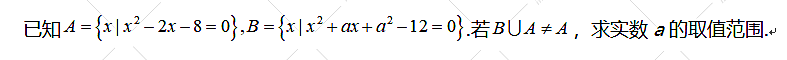 【解析】
【解析】 【答案】
【答案】 12.分段函数画图
12.分段函数画图 【答案】
【答案】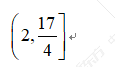 【解析】
【解析】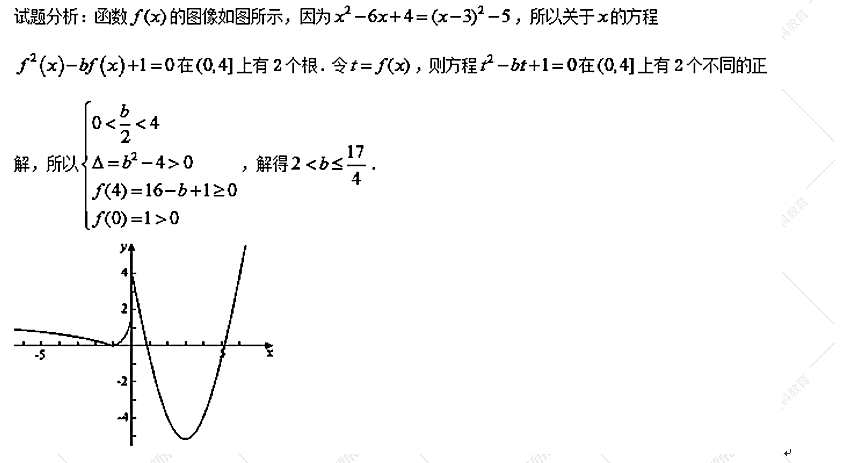 【方法点睛】
【方法点睛】

新东方石家庄学校 (微信号:helloxdf)
及时获取本地权威教育资讯,随时随地的贴身学习顾问,英语学习的好帮手、课程规划的好助手!
相关推荐
版权及免责声明
①凡本网注明"稿件来源:新东方"的所有文字、图片和音视频稿件,版权均属新东方教育科技集团(含本网和新东方网) 所有,任何媒体、网站或个人未经本网协议授权不得转载、链接、转贴或以其他任何方式复制、发表。已经本网协议授权的媒体、网站,在下载使用时必须注明"稿件来源:新东方",违者本网将依法追究法律责任。
② 本网未注明"稿件来源:新东方"的文/图等稿件均为转载稿,本网转载仅基于传递更多信息之目的,并不意味着赞同转载稿的观点或证实其内容的真实性。如其他媒体、网站或个人从本网下载使用,必须保留本网注明的"稿件来源",并自负版权等法律责任。如擅自篡改为"稿件来源:新东方",本网将依法追究法律责任。
③ 如本网转载稿涉及版权等问题,请作者见稿后在两周内速来电与新东方网联系,电话:010-60908555。